K-means聚类算法原理

0 前言

聚类是数据处理中常用的分析方法，此处简单介绍下K-means聚类算法原理。

1 K-means算法

1.1 算法简介

K-means标准算法是1957 年史都华·劳埃德(Stuart Lloyd)作为一种脉冲码调制的技术所提出，但直到1982年才被贝尔实验室公开出版在“ IEEE Transactions on Information Theory”中，原始文献为“Least square quantization in PCM”。术语“k-均值”于1967年才被詹姆斯·麦昆(James MacQueen) 在文献“Some methods for classification and analysis of multivariate observations”中提出，描述 K-means算法的完整理论并进行了详细的研究。

1.2 算法思想

K-means算法，又称K均值算法，其中K表示聚类簇数，means表示取每个簇所有数据的均值作为该簇的中心（或者称质心）。K-means算法的核心思想是将数据集中的n个对象划分为K个聚类，使得每个对象到其所属聚类的中心（或称为均值点、质心）的距离之和最小。这里所说的距离通常指的是欧氏距离，但也可以是其他类型的距离度量。

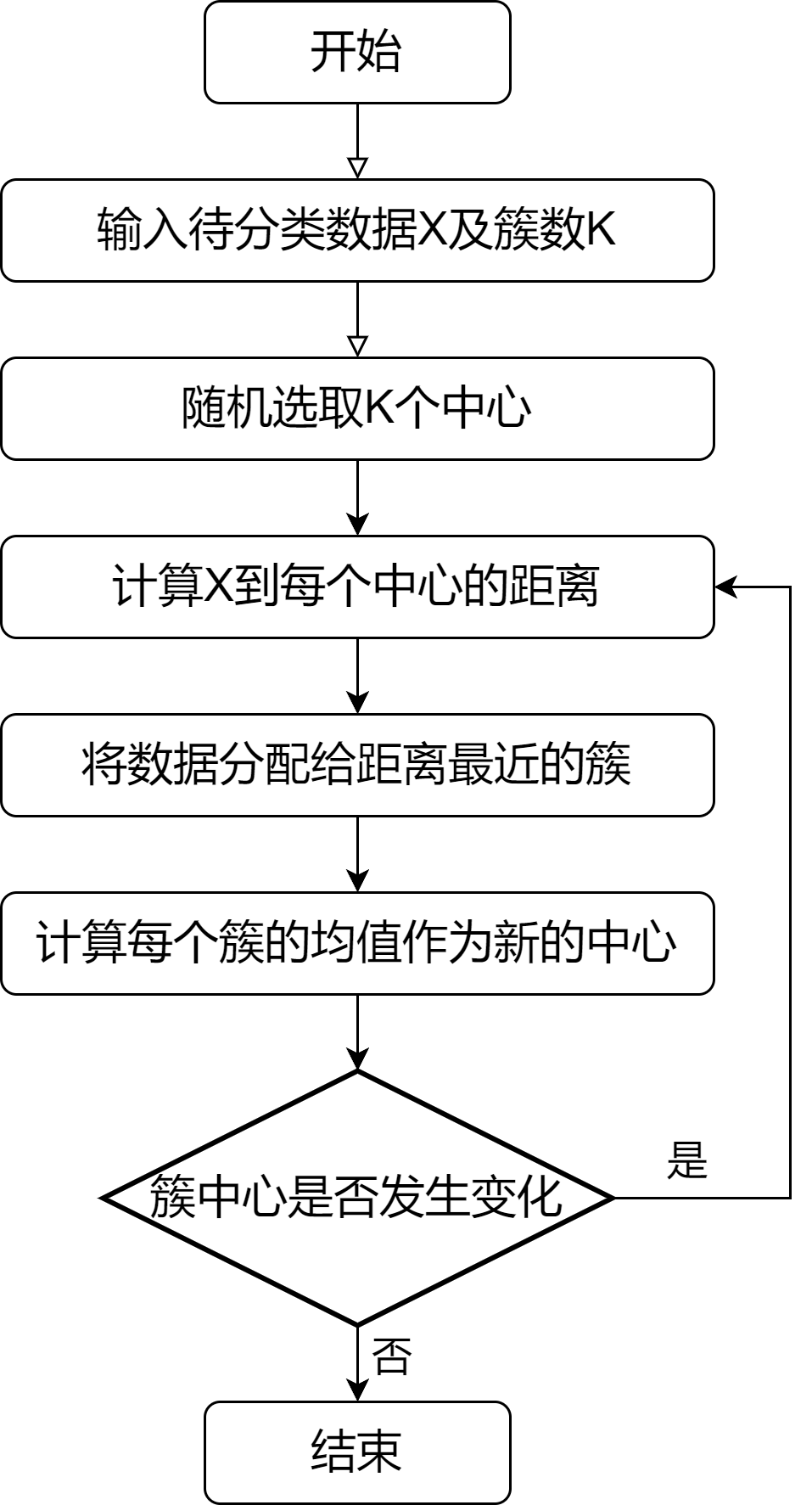
1.3 算法流程

对于待分类的数据X，随机选取K个簇中心
计算各个数据与各个簇中心的“距离”，并将各个数据划分至相距最近的簇
根据划分好的簇，计算每个簇的数据均值作为新的簇中心
重新计算所有数据与新的簇中心的“距离”，并重新分类
重复上述步骤，直至收敛

1.4 数学表达

假设存在一系列散点$X_i = (x_i,y_i)$，需要将其划分至$K$个簇
随机选择$K$个簇中心$(x_j,y_j)$，其中$j=1,2,\dots,K$
计算$X_i$到各个簇中心的欧式距离（也可以是其他距离，此处以欧式距离为例），并将$X_i$划分至$r_{i,j}$最小的簇$S_k$

$$
r_{i,j} = \sqrt{(x_i-x_j)^2 + (y_i - y_j)^2}, \quad j=1,2,\dots,K.
$$

重新计算每个簇的均值作为新的簇中心

$$
x_k = \sum_{x_i \in S_k} x_i / N(S_k), \quad y_k = \sum_{y_i \in S_k} y_i / N(S_k), \quad k = 1,2,\dots,K.
$$

其中$S_k$表示第$k$个簇所包含的数据，$N(S_k)$表示第$k$个簇所包含的数据个数。

重复上述步骤，直至新的簇中心与旧的簇中心没有差异

1.5 实例演示

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification

# 定义数据集
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=1, n_redundant=0, n_clusters_per_class=1, random_state=1)

# 根据欧氏距离将数据X分成两类
def rho_p1_p2(X,p1,p2):
    nums = X.shape[0]
    l1 = []
    l2 = []
    for idx in np.arange(nums):
        rho1 = np.linalg.norm(X[idx,:] - p1)
        rho2 = np.linalg.norm(X[idx,:] - p2)
        if rho1<rho2:
            l1.append(idx)
        else:
            l2.append(idx)

    return l1,l2

# 随机中心一
p1 = np.array([-2,-2])
# 随机中心二
p2 = np.array([2,2])
# 绘图
plt.figure(figsize=[15,8],dpi=300)
# 第一幅图为原始数据
plt.subplot(2,3,1)
plt.scatter(X[:,0],X[:,1])
for idx in np.arange(20):
    # 根据当前簇中心进行分类
    l1,l2 = rho_p1_p2(X,p1,p2)
    # 计算新的簇中心
    tmp1 = np.mean(X[l1,:],0)
    tmp2 = np.mean(X[l2,:],0)
    # 每进行一次分类绘制一次分类后的图像
    plt.subplot(2,3,idx+2)
    plt.scatter(X[l1,0],X[l1,1])
    plt.scatter(X[l2,0],X[l2,1])
    # 判断中心是否发生变化
    if np.linalg.norm(tmp1-p1)<1e-6 and np.linalg.norm(tmp2-p2)<1e-6:
        print(idx)
        break
    # 将簇中心替换为新的簇中心
    p1 = tmp1
    p2 = tmp2
plt.show()

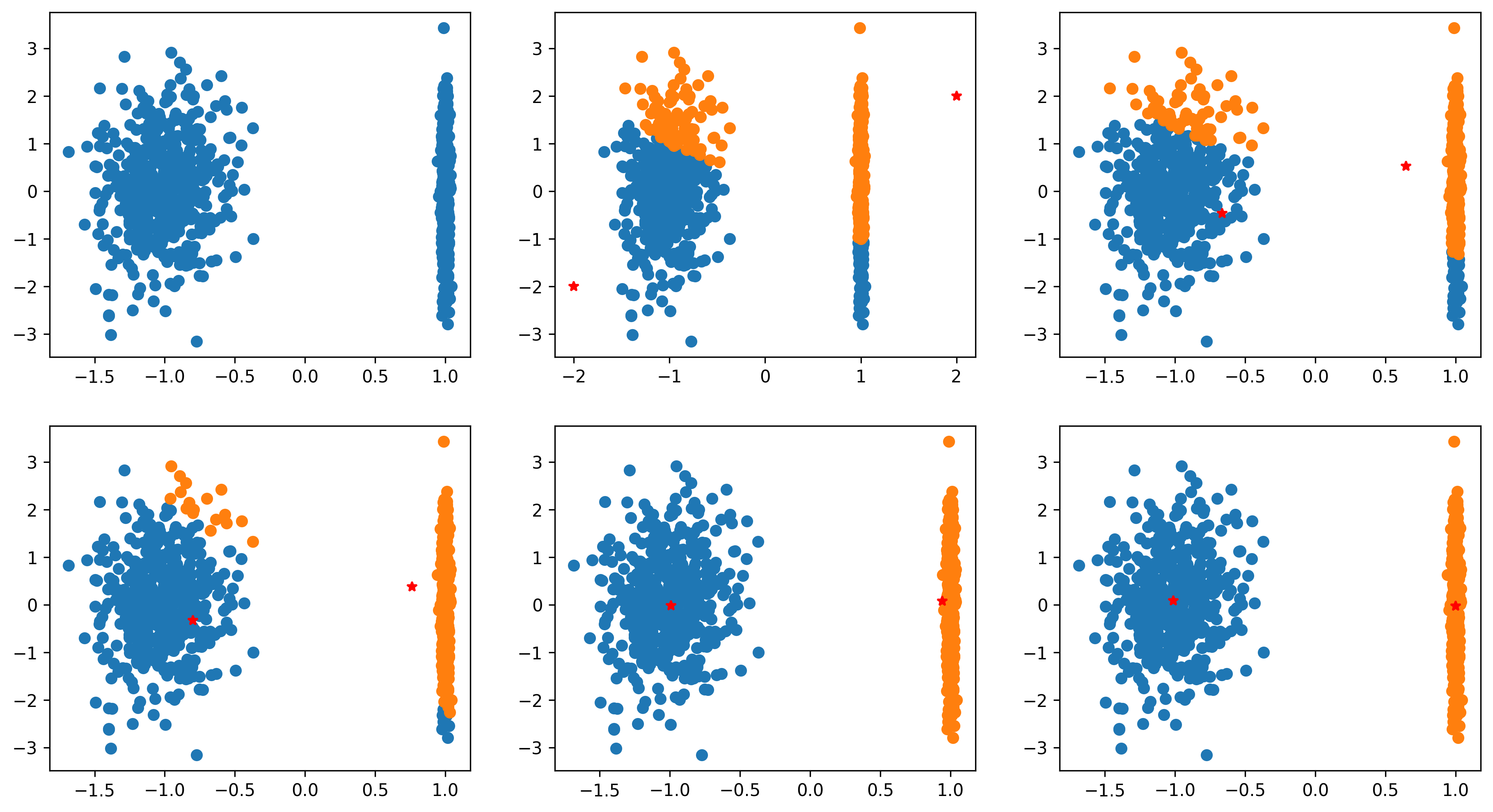
可以看出随着迭代此次数的增加，数据逐渐被分为两类。

2 拓展

2.1 “距离”计算方法

曼哈顿距离（Manhattan Distance）

$$
d(x,y) = \sum_{i=1}^n \vert x_i - y_i \vert
$$

欧几里得距离（Euclidean Distance）

$$
d(x,y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}
$$

切比雪夫距离（Chebyshev Distance）

切比雪夫距离起源于国际象棋中国王的走法，国际象棋中国王每次只能往周围的8格中走一步，那么如果要从棋盘中A格(x1,y1)走到B格(x2,y2)最少需要走几步？你会发现最少步数总是max(|x2-x1|,|y2-y1|)步。
$$
d(x,y) = \max \vert x_i - y_i \vert
$$

闵氏距离（Minkowski Distance）

对于点$x=(x_1,x_2,\dots,x_n)$ 与点$y=(y_1,y_2,\dots,y_n)$，闵氏距离可以用下式表示：
$$
d(x,y) = \left( \sum_{i=1}^n \vert x_i - y_i \vert^p \right)^{1/p}
$$
闵氏距离是对多个距离度量公式的概括性的表述，p=1退化为曼哈顿距离；p=2退化为欧氏距离；切比雪夫距离是闵氏距离取极限的形式。