高频传播特性的等效关系
0 前言
短波通信是一种常见的通信方式,其利用高频(High Frequency,HF)电磁波在电离层和地面之间的一次或多次反射,最远可将信号传至上万公里。在这个过程中,可以认为电离层和地面形成了类似“波导管”的结构。
在短波通信中,为了简化计算,通常会使用一些等效关系,这里将根据参考文献[1]中的内容,对这些等效关系进行介绍。
1 平面地球和平面电离层
1.1 “割线定律” - The "Secant Law"
在本节中,我们将考虑两个波的频率、虚拟路径和吸收之间存在的关系,一个波以斜入射反射,另一个波以垂直入射反射,二者的反射发生在相同的真实高度。为此,考虑以如下图所示的角度入射到平面电离层上的射线,其中电子密度随高度增加,从而发生全内反射。
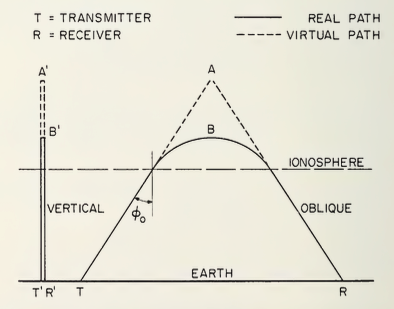
Refs [1] 图4.1 平面地球与平面电离层的等效定理
在没有碰撞和外加磁场的情况下,在等离子体频率为$f_N$的水平高度上,频率为$f$的波的折射率$\mu$由下式给出:
$$ \mu^2 = 1 - \left( \frac{f_N}{f} \right)^2 \tag{1} $$ 在反射层应用斯涅尔定律(Snell's law),即$\mu = \sin \phi_0$,可知 $$ f_N = f \cos \phi_0 $$ 如果$f_\nu$是与斜入射频率$f$在相同的真实高度(即相同的等离子体频率)上以垂直入射反射的频率,则$f_\nu =f_N$。因此 $$ f_\nu = f \cos \phi_0 \qquad {\rm or} \qquad f = f_\nu \sec \phi_0 \tag{2} $$ 该频率称为“等效垂直入射频率”,对应于$f$。上式中第二个式子就是所谓的割线定律。上述结果表明,在斜入射下,电离层反射的频率比正常入射时高得多。1.2 Breit和Tuve定理 - Breit and Tuve's Theorem
另一个比较重要的关系称为Breit和Tuve定理。其中表示发射机T与接收机R之间传输的群(或等效)路径$P'$由等效三角形TAR的长度给出,即:
$$ P' = TA + AR \tag{3} $$ 这可以通过以下论证来证明: $$ P' = \int_{TBR} \frac{ds}{\mu} = \int \frac{dx}{\mu \sin \phi} = \frac{1}{\sin \phi_0} \int dx = \frac{TR}{\sin \phi_0} = TA + AR $$ 请注意,反射的真实高度B总是小于A处的等效高度。应该记住,只有当发送者和接收者位于电离层之外时(3)式才成立。如果发射机和接收机位于电离层内,即折射率为$\mu_1$的水平高度上,则(3)式的右侧必须除以$\mu_1$,这样$P'$仍然意味着群传播时间乘以自由空间速度。
1.3 马丁(等效路径)定理 - Martyn's (Equivalent Path) Theorem
如果$f$和$f_\nu$是从同一实际高度斜向和垂直反射的波的频率,则垂直反射信号的虚高等于斜向信号的等效三角路径的高度。
考虑等离子体频率为$f_N$的相同实际高度下,斜波和垂直波的折射率为$\mu_{ob}$和$\mu_\nu$,我们有
$$ \mu_{ob}^2 = 1 - \left( \frac{f_N}{f} \right)^2 \qquad {\rm and} \qquad \mu_\nu^2 = 1 - \left( \frac{f_N}{f \cos \phi_0} \right)^2 \tag{4} $$根据斯涅尔定律(Snell's law)可知$\mu_{ob} \sin \phi = \sin \phi_0$。联立这些方程可以得到
$$ \mu_{ob} \cos \phi = \mu_\nu \cos \phi_0 \tag{5} $$ 斜测信号的群路径为 $$ P' = \int_{TBR} \frac{ds}{\mu_{ob}} = 2 \int_0^{h_r} \frac{dh}{\mu_{ob} \cos \phi} = \frac{2}{\cos \phi_0} \int_0^{h_r} \frac{dh}{\mu_\nu} = \frac{2}{\cos \phi_0} h_\nu' $$ 其中 $$ h_\nu' = \frac{1}{2} P' \cos \phi_0 = \frac{1}{2} (TA + AR) \cos \phi_0 = AD $$ 因此 $$ P'(f) = h'(f_\nu) \sec \phi_0 \tag{6} $$ 这个定理表达了斜入射波的虚反射高度与等效垂直波的虚反射高度相等的重要关系。1.4 马丁(吸收)定理 - Martyn's (Absorption) Theorem
略。
$$ \tag{7} $$ $$ \tag{8} $$2 电离层曲率的影响
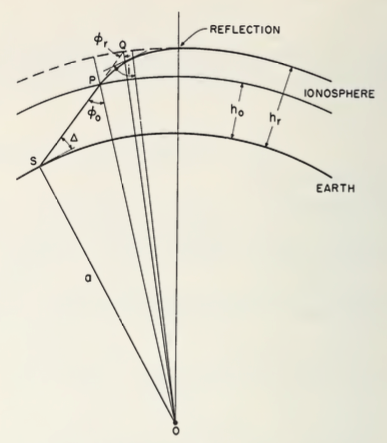
Refs [1] 图4.2 斜入射射线几何图像
在弯曲的电离层中,斯涅耳定律的形式是
$$ \mu r \sin i = \mu_0 r_0 \sin i_0 \tag{9} $$ 式中$r$为从地心到折射率为$\mu$处的半径矢量的长度,半径矢量与光线夹角为$i$,如上图所示,图中$\mu_0$、$r_0$和$i_0$为任意参考值。以地面为参照,则有$\mu_0 = 1$、$r_0 = a$且$i_0 = (\pi/2) - \Delta$,其中$\Delta$为仰角。即 $$ \mu r \sin i = a \cos \Delta \tag{10} $$ 将式(1)代入式(10),使用$f_\nu$替换$f_N$,给出了频率$f$与相同实际高度$h_r$反射的等效垂直频率$f_\nu$之间的关系。即 $$ \left( \frac{f_\nu}{f} \right)^2 = 1 - \left( \frac{a \cos \Delta}{a + h_r} \right)^2 \tag{11} $$ 设$\phi_r'$为未折射光线的延线与半径矢量在$h_r$处的夹角,如上图所示。从几何关系中可以得到 $$ (a + h_r) \sin \phi_r = a \cos \Delta \tag{12} $$ 因此 $$ f_\nu = f \cos \phi_r \tag{13} $$ 由式(11)和式(13)可以看出,等效频率不仅与$\Delta$有关,而且与反射高度$h_r$有关。$f_\nu$可以用(6)式或(7)式来定义,而不是用反射高度来定义,但与平面电离层的情况不同,$f_\nu$的值将取决于定义。


评论区